うちの庭は、狭いスペースに植木・畑・花壇が混在していて、一日中日が当たっているスペースというのがありません。太陽の動きを解析して日当たりチェックをできないものかな、といろいろ調べていると、こんな論文に出会いました:「魚眼レンズを用いた局所的な日照時間推定に関する検討 (PDF)」(星野佑輔ほか、釧路高専紀要 2017, 50, 72-75)。なるほど、魚眼レンズってこんな使い方があるんだ。
さっそくスマホ用の魚眼レンズを取り寄せてみました。100均でも売ってるらしいんですが、あんまりちゃちいのもどうかなと思って、それなりの値段のものを選びました。
画面で確認しながら撮影したいので、インカメラに取り付けます。スマホは Zenfone 5 で、問題なく取り付けできます。三脚は使いませんが、スマホホルダーを取り付けておくと、クリップとスマホホルダーで本体がほぼ水平に置けます。水平を出すのは大事なので、水準器を貼り付けたベニヤ板の上に置きます。
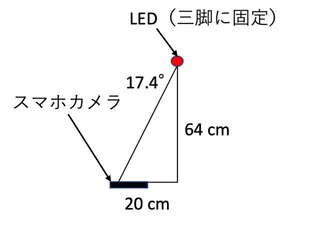
写っている範囲を特定するため、校正をやりました。LEDライトを点灯する回路を組み立てて(久しぶりにブレッドボードを持ち出した)、三脚の上に固定し、下のような配置にして撮影します。三脚の位置を動かしてスマホとLEDの水平距離を変えれば、スマホから見た仰角を変えながら写真撮影ができます。
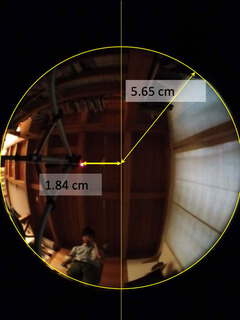
写真を適当な倍率で PowerPoint ファイルに貼り付け、丸い画像の輪郭に合わせて円を書きます。その円の半径と、中心から LED の像までの距離を測ると、下のようになりました。
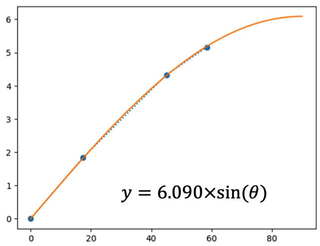
仰角を3点設定して同じように距離を測り、校正曲線を書きました。周辺に近づくほど圧縮されているので、正射影方式に近いようです(参考:「魚眼レンズ、実は人眼レンズ?」Optical Learning Blog, 2022/5/24)。式のθは、天頂角(90°-仰角)です。
校正曲線は Python/Jupyter Notebook で作成。Python を使うのにもだいぶ慣れてきました。
from scipy.optimize import curve_fit
import numpy as np
import matplotlib.pyplot as plt
import math
x_obs = np.array([0, 17.4, 45.0, 58.4])
y_obs = np.array([0, 1.84, 4.33, 5.16])
def func(x, a):
y = np.zeros_like(x)
for i in range(x.shape[0]):
xi = x[i]
y[i] = a * math.sin(xi / 180.0 * math.pi)
return y
popt, pcov = curve_fit(func, x_obs, y_obs, p0=[0.5])
print(popt)
fig, ax = plt.subplots()
x_cal = np.linspace(0, 90)
y_cal = func(x_cal, popt[0])
ax.plot(x_obs, y_obs, "o:")
ax.plot(x_cal, y_cal)
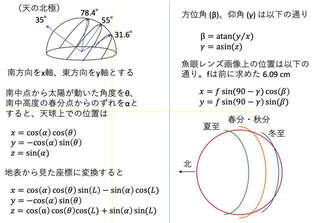
次に、太陽の通り道を描画します。中学理科の内容だけど、忘れてる! いろいろ調べながら考えました。
これも描画は Python でやりました。
import numpy as np
import matplotlib.pyplot as plt
import math
th = np.linspace(-90, 90)
L = 35.0 # 観測地点の緯度
f = 6.09
def func(th, a):
x = []
y = []
z = []
Lr = L * math.pi / 180.0
ar = a * math.pi / 180.0
for i in range(th.shape[0]):
ti = th[i] * math.pi / 180.0
xi = math.cos(ar) * math.cos(ti) * math.sin(Lr) - math.sin(ar) * math.cos(Lr)
yi = -math.cos(ar) * math.sin(ti)
zi = math.cos(ar) * math.cos(ti) * math.cos(Lr) + math.sin(ar) * math.sin(Lr)
azimuth = math.atan2(yi, xi)
altitude = math.asin(zi)
if altitude >= 0.0:
xj = f * math.sin(math.pi * 0.5 - altitude) * math.cos(azimuth)
yj = f * math.sin(math.pi * 0.5 - altitude) * math.sin(azimuth)
x.append(xj)
y.append(yj)
return np.array(x), np.array(y)
x1, y1 = func(th, -23.4)
x2, y2 = func(th, 0)
x3, y3 = func(th, 23.4)
s = np.linspace(-math.pi, math.pi)
x = [5.65 * math.cos(_) for _ in s]
y = [5.65 * math.sin(_) for _ in s]
fig, ax = plt.subplots(figsize=(4,4))
ax.set_xlim([-7, 7])
ax.set_ylim([-7, 7])
ax.plot(x1, y1)
ax.plot(x2, y2)
ax.plot(x3, y3)
ax.plot(x, y)
plt.gca().axis('off')
plt.savefig("output.pdf", transparent="True")
スマホを真北に向けて、ナツミカンの前の畑の地面で写真をとり、太陽軌道を重ねてみました。右上の木はウメ、右下の木はナツミカンです。夏至の日はまあまあ長く日が当たるけど、春分・秋分の頃にはナツミカンの影に入ってしまうことがわかります。畑の上にかぶさるように枝が伸びてるもんなあ。今後の剪定プランはこれを見ながら検討しましょう。