(2007/07/04 記)
OpenGL を Mac OS X で使う一般的な方法については世の中にいくらでも情報があるので、「分子の図を描く」目的に特化してメモ。OpenGL というより 3D グラフィックス一般、というより単なる3次元幾何学のメモになってしまうかも。

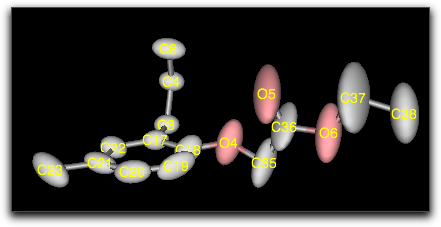
分子の構造をX線を使って調べる時、各原子の位置がある平均値の周りに三次元正規分布していると仮定して解析するのが通例である。三次元正規分布では、等確率の点を結んだ面は楕円体になるので、任意の向き・大きさの楕円体が表示できることが望ましい。
OpenGL で楕円体を表示するには、glutSolidSphere() で球を表示して、座標変換して楕円体にするのが簡単。自分でメッシュの点を計算して三角形の集まりを描くことも考えたが、計算がえらい煩雑になるのでやめた。
static void drawEllipsoid(const float *p, const float *v1, const float *v2, const float *v3, int sect) { GLfloat mat[16]; mat[0] = v1[0]; mat[1] = v1[1]; mat[2] = v1[2]; mat[3] = 0; mat[4] = v2[0]; mat[5] = v2[1]; mat[6] = v2[2]; mat[7] = 0; mat[8] = v3[0]; mat[9] = v3[1]; mat[10] = v3[2]; mat[11] = 0; mat[12] = p[0]; mat[13] = p[1]; mat[14] = p[2]; mat[15] = 1; glMatrixMode(GL_MODELVIEW); glPushMatrix(); glMultMatrixf(mat); glEnable(GL_NORMALIZE); glutSolidSphere(1, sect, sect); glDisable(GL_NORMALIZE); glPopMatrix(); }
p は楕円体の中心。v1, v2, v3 は楕円体の主軸で、互いに直交しており、p±v1, p±v2, p±v3なる点が楕円体の表面上にある。上のコードでは、原点中心の単位球を描いて、(1,0,0)→v1, (0,1,0)→v2, (0,0,1)→v3 と座標変換して p だけ平行移動している。
けみかるな人のためのメモ:X線構造解析の温度因子を B = (bij) で表すと、B は対称行列で、直交座標で表した主軸の方向は対称行列 AT・B-1・A の固有ベクトルで表される。A は直交座標を結晶座標に変換する行列。各主軸方向の長さは、固有値をλとすると 1/sqrt(λ/2π2) となる。習慣通り 50% の確率楕円体で描く時は、これにさらに 1.5382 を掛ける。
NSOpenGLView の上に透明な NSView をかぶせて、その上にラベルを描こうと思ってもうまくいかない(できる方法があるのかも知れないが、見つけることができなかった)。そこで、OpenGL のテクスチャを利用してラベルを表示するようにした。
Apple のサンプルコードで Cocoa OpenGL というのがあって、その中の StringTexture.m というのがまさしく OpenGL 画面にテキストを書くクラス。ただし、指定イニシャライザの - (id) initWithAttributedString:(NSAttributedString *)attributedString withTextColor:(NSColor *)text withBoxColor:(NSColor *)box withBorderColor:(NSColor *)border は一見テキストカラーを指定できそうなのに、text 引数は効果なく attributedString の属性として指定した色が使われる。何を渡しても文字色が黒のままなので3日悩んじゃったじゃないか。
StringTexture をそのまま使うと、OpenGL モデルの手前にすべてのラベルが表示される。これだと、ぐるぐる回した時にどのラベルとどの楕円体が対応しているのかわかりにくい。他の楕円体に隠れてしまうときはラベルも一緒に隠れてくれると都合がよい。それには、デプスバッファを有効にして、楕円体のすぐ手前の Z 座標を与えてラベルを書けばよい。StringTexture をサブクラス化するのが素直なやり方だが、objective C ならこんなやり方もある。
@implementation StringTexture (drawWithDepth) - (void) drawAtPoint:(NSPoint)point withDepth: (float)z { if (!texName) [self genTexture]; if (texName) { NSRect bounds = NSMakeRect(point.x, point.y, texSize.width, texSize.height); glBindTexture(GL_TEXTURE_RECTANGLE_EXT, texName); glBegin(GL_QUADS); glTexCoord3f(0.0f, 0.0f, z); glVertex3f(bounds.origin.x, bounds.origin.y, z); /* snip */ glEnd(); } } @end
あとは、各楕円体に対して「すぐ手前」の Z 座標を求める方法だが、これが意外と厄介だった。楕円体の主軸が視線と平行だったら、視線と楕円面との交点の Z 座標を使えばよいが(下図左)、一般の楕円体だとそうはいかない(下図中)。下図右のように、視線に垂直な楕円面の接平面を使う必要がある。
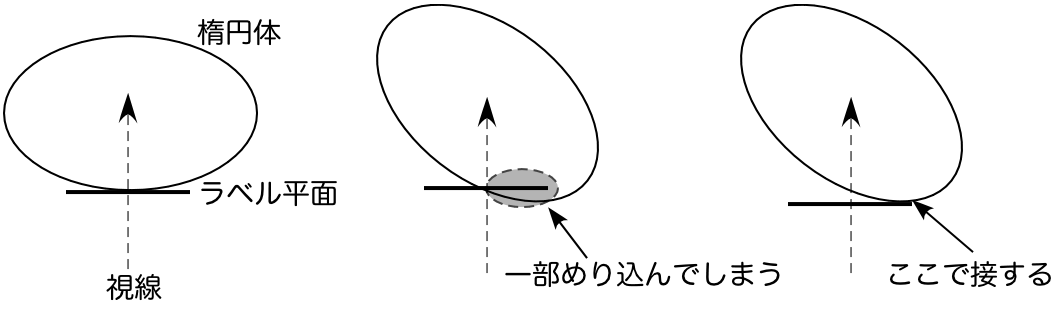
ちゃんと式誘導して一発で計算するのが正しいのだろうが、なんとなく間違えそうだったので、「視線に垂直な2本のベクトルを求める」→「楕円体が単位球になるよう座標変換する」→「さきほどの2本のベクトルを変換して、それらを含む単位球の接平面を求める」→「座標を元に戻す」→「視線と接平面の交点を求める」という回りくどいやり方を採用した。実は他の目的で座標変換の行列が計算してあったりするので、コード量は意外に少なくてすんだ。